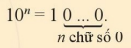Trang 22
Vi khuẩn E. coli trong điều kiện nuôi cấy thích hợp cứ 20 phút lại phân đôi một lần.
(Nguồn: Sinh học 10, NXB Giáo dục Việt Nam, 2010)

Giả sử lúc đầu có 1 vi khuẩn. Sau 120 phút có bao nhiêu vi khuẩn?
Hình ảnh phóng to của vi khuẩn E. coli
I. PHÉP NÂNG LÊN LUỸ THỪA
1 Người ta viết gọn tổng của nhiều số hạng bằng nhau thành phép nhân, chẳng hạn: 2+2+2+2+2+2=2.6.
Ta cũng có thể viết gọn tích của nhiều thừa số bằng nhau, chẳng hạn: 2.2.2.2.2.2 được viết gọn là 26. Số 2 gọi là cơ số và số 6 gọi là số mũ. Ta có: 26 = 64.
| Luỹ thừa bậc n của a, kí hiệu an, là tích của n thừa số a
Số a được gọi là cơ số, n được gọi là số mũ. Quy ước: a1 = a. |
Phép nhân nhiều thừa số bằng nhau gọi là phép nâng lên luỹ thừa.
Chú ý: an đọc là “a mũ n” hoặc “a luỹ thừa n” hoặc “luỹ thừa bậc n của a";
a2 còn được gọi là “a bình phương” hay “bình phương của a";
a3 còn được gọi là “a lập phương” hay “lập phương của a".
Ví dụ 1 Đọc các luỹ thừa sau và nêu cơ số, số mũ của chúng:
a) 37;
b) 53.
Trang 23
Giải
a) 37 đọc là “ba mũ bảy” hoặc “ba luỹ thừa bảy” hoặc “luỹ thừa bậc bảy của ba"; cơ số là 3 và số mũ là 7.
b) 53 đọc là “năm mũ ba” hoặc “năm luỹ thừa ba” hoặc “luỹ thừa bậc ba của năm” hoặc “năm lập phương”; cơ số là 5 và số mũ là 3.
Ví dụ 2 Viết các tích sau dưới dạng luỹ thừa:
a) 2 . 2 . 2 . 2 . 2:
b) 3 . 3 . 3 . 3 . 3 . 3.
Giải
a) 2.2.2.2.2=25.
b) 3.3.3.3.3.3-36.
| 1 Viết và tính các luỹ thừa sau: a) Năm mũ hai; b) Hai luỹ thừa bảy; c) Luỹ thừa bậc ba của sáu. |
Ví dụ 3 Tính các luỹ thừa sau:
a) 10³;
b) 106.
|
Với n là số tự nhiên khác 0, ta có: 10n=1 0... 0. n chữ số 0 |
Giải
a) 103 10.10.10 = 1000.
b) 106 = 10.10.10.10.10.10 1 000 000,
Vi dụ 4
| 2) Viết các số sau dưới dạng luỹ thừa với cơ số cho trước: a) 25, cơ số 5; b) 64, cơ số 4. |
a) Viết 16 dưới dạng luỹ thừa của 2.
b) Viết 100 000 dưới dạng luỹ thừa của 10.
Giải
a) 16 = 2.2.2.2 = 24.
b) 100 000 = 10.10.10.10.10 = 105.
II. NHÂN HAI LUỸ THỪA CÙNG CƠ SỐ
2 So sánh: 23. 24 và 27.

23=2.2.2 là tích của ba thừa số 2.
24=2.2.2.2 là tích của bốn thừa số 2.
Kết quả của 23. 24 là tích của bảy thừa số 2, tức là 23. 24 = 27-23+4.
Trang 24
| Khi nhân hai luỹ thừa cùng cơ số, ta giữ nguyên cơ số và cộng các số mũ: am.an=am+n |
Ví dụ 5 Viết kết quả mỗi phép tính sau dưới dạng một luỹ thừa:
a) 32.36,
b) 5.56.
Giải
a) 32.36 = 32+6 = 38
b) 5 . 56 = 51 . 56= 5 1+6=57
| 3. Viết kết quả mỗi phép tính sau dưới dạng một luỹ thừa: a) 25. 64; b) 20 . 5 . 103. |
III. CHIA HAI LUỸ THỪA CÙNG CƠ SỐ
3 So sánh: 25: 23 và 22.

25 = 2.2.2.2.2 là tích của năm thừa số 2.
23 = 2.2.2 là tích của ba thừa số 2.
Kết quả của 25 : 23 là tích của hai thừa số 2,
tức là 25: 23 = 22-25-3.
| Khi chia hai luỹ thừa cùng cơ số (khác 0), ta giữ nguyên cơ số và trừ các số mũ: am: an=am-n(a ≠ 0; m≥n). Quy ước: a0 = 1 (a ≠ 0). |
Ví dụ 6 Viết kết quả mỗi phép tính sau dưới dạng một luỹ thừa:
a) 46: 42,
b) 53: 125.
Giải
a) 46 : 42 = 46-2 = 44
b) 53 : 125 = 53: 53= 53 - 3= 50.
| 4. Viết kết quả mỗi phép tính sau dưới dạng một luỹ thừa: a) 65:6; b) 128: 23. |
BÀI TẬP
1. Viết các tích sau dưới dạng luỹ thừa:
a) 5.5.5.5;
b) 9.9.9.9.9.9.9;
c) 7.7.7.7.7;
d) a.a.a.a.a.a.a.a.
Trang 25
2. Xác định cơ số, số mũ và tính mỗi luỹ thừa sau: 25, 52,92, 110, 101,
3. Viết các số sau dưới dạng luỹ thừa với cơ số cho trước:
a) 81, cơ số 3;
c) 64, cơ số 2;
b) 81, cơ số 9;
d) 100 000 000, cơ số 10.
4. Viết kết quả mỗi phép tính sau dưới dạng một luỹ thừa:
a) 34,35;
16,29;
16,32;
b) 128: 12;
243: 34;
109: 10 000;
c)
4.86.2.83;
122.2.123.6;
63.2.64.3.
5. So sánh:
a) 32 và 3. 2;
b) 23 và 32;
c) 33 và 34.
6. Khối lượng của Mặt Trời khoảng 1988 550. 1021 tấn, khối lượng của Trái Đất khoảng 6. 1021 tấn. (Nguồn: http://nssdc.gsfc.nasa.gov) Khối lượng của Mặt Trời gấp khoảng bao nhiêu lần khối lượng của Trái Đất?
7. Đố. Cho biết 112 = 121; 1112 = 12 321.
Hãy dự đoán 1 1112 bằng bao nhiêu. Kiểm tra lại dự đoán đó.
CÓ THỂ EM CHƯA BIẾT
Vi khuẩn lị E. coli
Ê-sơ-ric-kiơ cô-li (Escherichia coli, viết tắt: E. coli) là một loài vi khuẩn gây ra bệnh tiêu chảy.
Thê-ô-đo Ê-sơ-ric (Theodor Escherich) là người đầu tiên phát hiện ra loài vi khuẩn này vào năm 1885 khi ông nghiên cứu về các trẻ em bị bệnh tiêu chảy. Phát minh này đã đưa ông trở thành một trong những nhà vi khuẩn học hàng đầu thời đó. Năm 1919, các nhà khoa học đã đặt tên loài này là Ê-sơ-ric-kiơ cô-li để vinh danh ông.
Ông còn phát hiện ra rằng nhiều bệnh thuộc lĩnh vực Nhi khoa thời đó có nguyên nhân do vi khuẩn gây ra, lây truyền chủ yếu qua con đường ăn uống. Vì thế, ông còn được coi là thầy thuốc Nhi khoa đầu tiên về bệnh truyền nhiễm ở trẻ em.
(Nguồn: https://vi.wikipedia.org/wiki)

Theodor Escherich (1857-1911)
 với n∈N*.
với n∈N*.